In the world of mathematics, the unit circle is a fundamental concept that plays a crucial role in understanding trigonometry. It is a circle with a radius of one, centered at the origin of a coordinate plane. When combined with the tangent function, the unit circle becomes an invaluable tool for solving complex problems and visualizing mathematical relationships. This guide aims to provide a comprehensive understanding of the unit circle with tangent, exploring its significance, applications, and how it can be utilized effectively in various fields.
The unit circle and tangent function are integral to trigonometry, offering a visual representation of angles and their corresponding trigonometric values. The unit circle allows for the seamless calculation of sine, cosine, and tangent values, making it an essential tool for students and professionals alike. By mastering the unit circle with tangent, one can unlock a deeper appreciation for the elegance and utility of mathematics in both theoretical and practical contexts.
Whether you're a student striving to excel in your math classes or a professional seeking to enhance your problem-solving skills, this guide will equip you with the knowledge and tools necessary to master the unit circle with tangent. With easy-to-understand explanations, practical examples, and useful tips, you'll be well on your way to becoming proficient in this vital mathematical concept.
Read also:Reflective Moments The Impact Of If I Turn Back Time
Table of Contents
- What is the Unit Circle?
- Understanding the Tangent Function
- How Does Tangent Relate to the Unit Circle?
- Using the Unit Circle to Find Tangent Values
- Visualizing Tangent on the Unit Circle
- Applications of Unit Circle with Tangent
- Common Mistakes and How to Avoid Them
- Advanced Concepts in Unit Circle and Tangent
- Unit Circle with Tangent in Real-World Scenarios
- Teaching Tips for Educators
- Unit Circle with Tangent and Technology
- How Can You Practice the Unit Circle with Tangent?
- Frequently Asked Questions
- Conclusion
What is the Unit Circle?
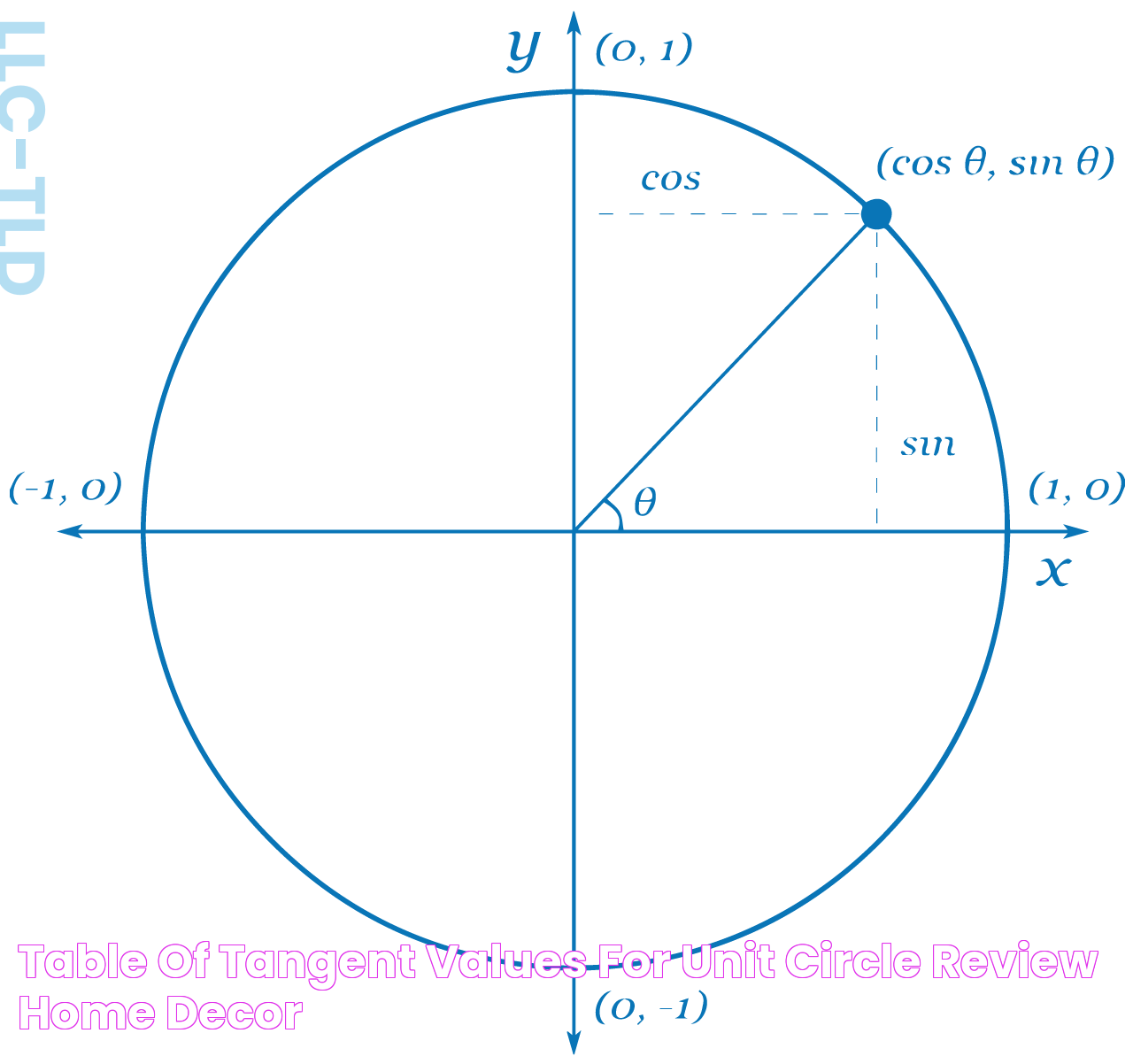
The unit circle is a fundamental concept in trigonometry, defined as a circle with a radius of exactly one unit, centered at the origin (0, 0) of a coordinate plane. This unique circle provides a simple method for understanding the relationships between angles and trigonometric functions such as sine, cosine, and tangent. The unit circle allows us to visualize these relationships in a straightforward and intuitive manner, making it an indispensable tool for students and mathematicians alike.
By using the unit circle, we can easily determine the sine and cosine of any angle. The x-coordinate of a point on the circle corresponds to the cosine of the angle, while the y-coordinate represents the sine of the angle. This makes it possible to calculate these values quickly and accurately, even for complex angles. Moreover, the unit circle helps us understand the periodic nature of trigonometric functions, providing a clear visual representation of their behavior as angles increase or decrease.
The unit circle also serves as a foundation for more advanced mathematical concepts, including calculus and analytic geometry. By mastering the unit circle, students can build a strong understanding of these subjects and develop the skills needed to tackle more challenging problems. In short, the unit circle is an essential tool for anyone studying mathematics, offering a simple yet powerful method for understanding trigonometric functions and their relationships.
Understanding the Tangent Function
The tangent function is one of the three primary trigonometric functions, alongside sine and cosine. It is defined as the ratio of the sine and cosine of a given angle, represented by the formula:
Tangent (tan) = Sine (sin) / Cosine (cos)
This relationship means that the tangent function can be derived from the unit circle, as both sine and cosine values can be easily determined from points on the circle. The tangent function is periodic, with a period of π, and exhibits unique behavior compared to sine and cosine functions.
Read also:All You Need To Know About The Poodle Schnauzer Mix The Perfect Companion
One of the most notable features of the tangent function is its asymptotic nature. Unlike sine and cosine, which have maximum and minimum values, the tangent function can approach positive or negative infinity. This occurs when the cosine value is zero, resulting in a division by zero in the tangent formula. These points, known as vertical asymptotes, occur at odd multiples of π/2 (90 degrees), such as π/2, 3π/2, etc.
The tangent function is particularly useful for solving problems involving right triangles, as it relates the opposite and adjacent sides of a triangle. By understanding the tangent function and its properties, students can develop a deeper comprehension of trigonometry and its applications in various fields.
How Does Tangent Relate to the Unit Circle?
The relationship between the tangent function and the unit circle is crucial for understanding trigonometry. By examining the unit circle, we can visualize how the tangent function behaves and determine tangent values for different angles. The unit circle provides a simple and intuitive method for calculating tangent values, as it allows us to easily determine the sine and cosine of any angle.
To find the tangent of an angle using the unit circle, we first identify the corresponding point on the circle. The x-coordinate of this point represents the cosine of the angle, while the y-coordinate represents the sine. By dividing the sine by the cosine, we can calculate the tangent value for the angle. This method is both efficient and accurate, making it an invaluable tool for students and professionals alike.
The unit circle also helps us understand the behavior of the tangent function, particularly its periodicity and asymptotic nature. By visualizing the unit circle, we can see how the tangent function approaches infinity at odd multiples of π/2, where the cosine value is zero. This provides a clear understanding of the function's unique properties and helps us avoid common pitfalls when working with tangent values.
Using the Unit Circle to Find Tangent Values
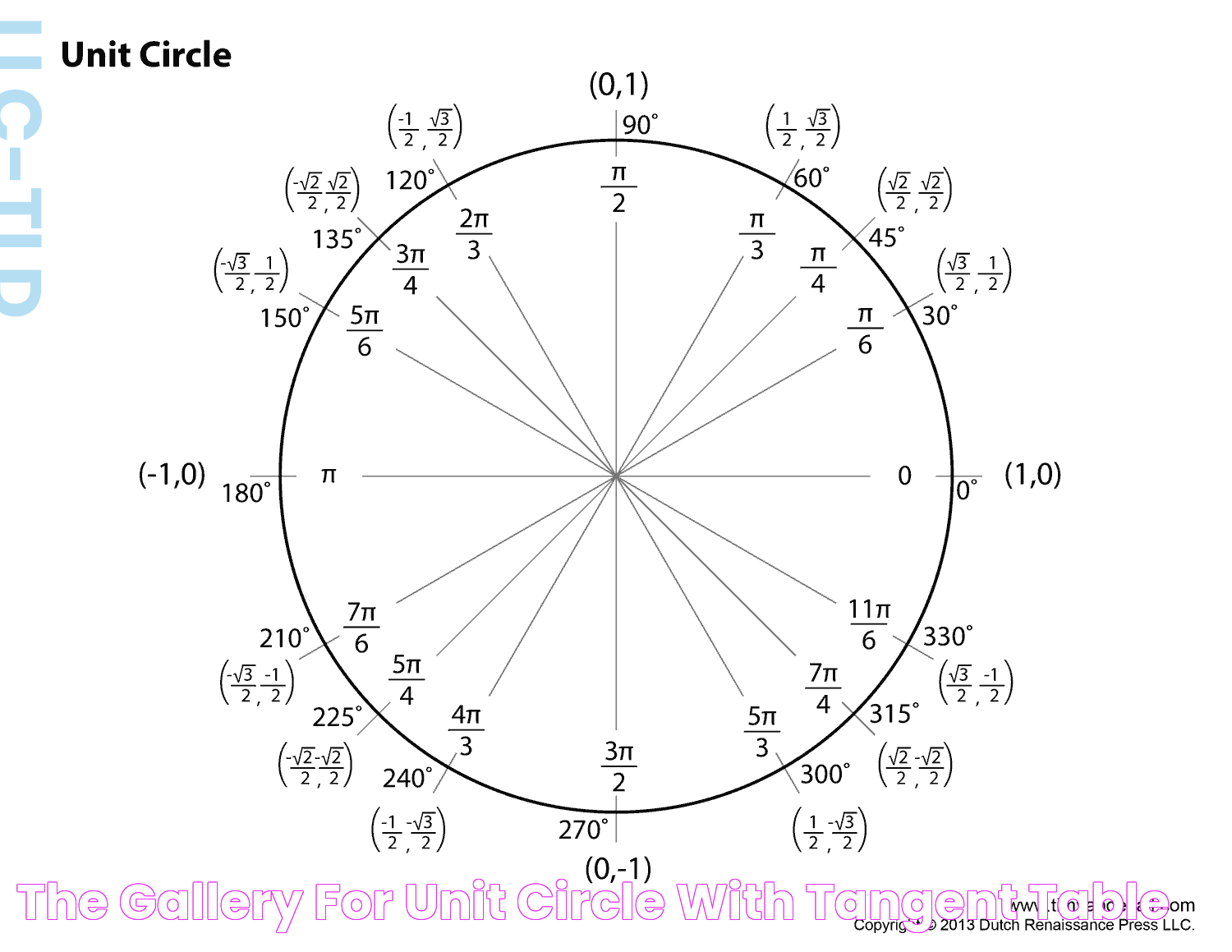
Finding tangent values using the unit circle is a straightforward process that can greatly simplify trigonometric calculations. To begin, we identify the angle for which we wish to find the tangent value and locate the corresponding point on the unit circle. This point's coordinates will provide the necessary sine and cosine values for the calculation.
- Determine the angle: Identify the angle for which you need to find the tangent value. Angles can be measured in degrees or radians, depending on the context.
- Locate the point on the unit circle: Find the point on the unit circle that corresponds to the given angle. This point's x-coordinate represents the cosine of the angle, while the y-coordinate represents the sine.
- Calculate the tangent value: Divide the y-coordinate (sine) by the x-coordinate (cosine) to find the tangent value for the angle. This simple formula allows for quick and accurate calculations.
By using the unit circle to find tangent values, students can develop a strong understanding of trigonometric functions and their relationships. This method not only simplifies calculations but also provides a visual representation of the function's behavior, making it easier to grasp complex concepts and identify potential errors.
Visualizing Tangent on the Unit Circle
Visualizing the tangent function on the unit circle is an effective way to understand its behavior and properties. By examining the unit circle, we can see how the tangent function relates to the sine and cosine functions and how it behaves as the angle changes. This visual representation can help students grasp complex trigonometric concepts and avoid common mistakes when working with tangent values.
To visualize the tangent function on the unit circle, consider the following steps:
- Identify the angle: Begin by identifying the angle for which you wish to visualize the tangent function. Angles can be measured in degrees or radians, depending on the context.
- Locate the point on the unit circle: Find the point on the unit circle that corresponds to the given angle. This point's x-coordinate represents the cosine of the angle, while the y-coordinate represents the sine.
- Draw the tangent line: Draw a line from the origin to the point on the unit circle, forming a triangle with the x-axis. The length of the line segment from the point to the x-axis represents the tangent value for the angle.
By visualizing the tangent function on the unit circle, students can develop a deeper understanding of its properties, such as its periodicity and asymptotic nature. This visual approach can also help identify potential errors and improve problem-solving skills, making it an invaluable tool for anyone studying trigonometry.
Applications of Unit Circle with Tangent
The unit circle with tangent has numerous applications in various fields, making it an essential tool for students and professionals alike. By understanding the relationships between angles and trigonometric functions, we can solve complex problems and gain valuable insights into a wide range of topics.
Some key applications of the unit circle with tangent include:
- Geometry: The unit circle is a fundamental concept in geometry, helping to describe the properties of angles and shapes. By mastering the unit circle with tangent, we can develop a deeper understanding of geometric relationships and solve complex problems with ease.
- Physics: Trigonometry plays a crucial role in physics, particularly in the study of waves, oscillations, and circular motion. The unit circle with tangent can help us analyze these phenomena and develop accurate models for predicting behavior.
- Engineering: Engineers frequently use trigonometry to design and analyze structures, systems, and machines. By understanding the unit circle with tangent, engineers can develop more efficient designs and improve the performance of their projects.
- Computer Science: Trigonometry is used in computer graphics, animation, and simulations to create realistic visual effects and models. The unit circle with tangent can help programmers and developers create more accurate and visually appealing representations.
These applications demonstrate the versatility and importance of the unit circle with tangent in various fields. By mastering this concept, students and professionals can unlock a wealth of opportunities and enhance their problem-solving skills in both theoretical and practical contexts.
Common Mistakes and How to Avoid Them
While the unit circle with tangent is a powerful tool for understanding trigonometry, it can also be challenging for students to master. Common mistakes can lead to errors in calculations and misunderstandings of the material. By identifying these mistakes and learning how to avoid them, students can improve their problem-solving skills and develop a deeper understanding of trigonometry.
Some common mistakes include:
- Incorrect angle measurement: Ensure that angles are measured accurately, in either degrees or radians, depending on the context. Misunderstanding the angle can lead to incorrect calculations and results.
- Misidentifying points on the unit circle: Double-check the coordinates of points on the unit circle to ensure they correspond to the correct angle. Incorrect points can lead to errors in sine, cosine, and tangent values.
- Confusing sine, cosine, and tangent: Remember that the sine is the y-coordinate, cosine is the x-coordinate, and tangent is the ratio of sine to cosine. Mixing up these functions can lead to incorrect calculations and misunderstandings.
- Overlooking asymptotes: Be aware of the vertical asymptotes in the tangent function, which occur at odd multiples of π/2. These points represent division by zero and can lead to errors in calculations.
By recognizing these common mistakes and taking steps to avoid them, students can improve their understanding of the unit circle with tangent and enhance their problem-solving skills. Practice and careful attention to detail are essential for mastering this powerful mathematical tool.
Advanced Concepts in Unit Circle and Tangent
Once students have a solid understanding of the unit circle with tangent, they can begin to explore more advanced concepts in trigonometry. These topics build upon the foundational knowledge of the unit circle and tangent function, providing a deeper understanding of their relationships and applications.
Some advanced concepts include:
- Inverse trigonometric functions: These functions, such as arcsine, arccosine, and arctangent, allow us to determine angles from given sine, cosine, or tangent values. Understanding inverse functions can help solve more complex problems and enhance problem-solving skills.
- Trigonometric identities: These are equations that express relationships between trigonometric functions, such as the Pythagorean identity or angle sum and difference identities. Mastering these identities can simplify calculations and provide valuable insights into trigonometric relationships.
- Complex numbers: Trigonometry plays a crucial role in understanding complex numbers, which include both real and imaginary components. By mastering the unit circle with tangent, students can develop a deeper understanding of complex numbers and their applications in various fields.
- Fourier analysis: This advanced mathematical technique uses trigonometric functions to analyze and decompose complex waveforms, making it an essential tool in fields such as signal processing, acoustics, and communications.
By exploring these advanced concepts, students can deepen their understanding of trigonometry and unlock new opportunities for problem-solving and analysis. The unit circle with tangent serves as a foundation for these topics, providing a strong basis for further study and exploration.
Unit Circle with Tangent in Real-World Scenarios
The unit circle with tangent is not just a theoretical concept; it has numerous real-world applications that demonstrate its importance and utility. By understanding how to apply the unit circle with tangent in practical scenarios, students and professionals can solve complex problems and gain valuable insights into a variety of fields.
Some real-world scenarios where the unit circle with tangent is applicable include:
- Navigation and GPS: Trigonometry is used in navigation systems to calculate distances, angles, and positions. By understanding the unit circle with tangent, we can develop more accurate models and enhance the precision of GPS systems.
- Architecture and construction: Architects and engineers use trigonometry to design and analyze structures, ensuring stability and safety. The unit circle with tangent can help create more efficient designs and improve the performance of construction projects.
- Physics: Trigonometry plays a crucial role in physics, particularly in the study of waves, oscillations, and circular motion. The unit circle with tangent can help us analyze these phenomena and develop accurate models for predicting behavior.
- Music and acoustics: Trigonometry is used in the analysis and synthesis of sound waves, helping to create more accurate and realistic audio representations. The unit circle with tangent can enhance our understanding of these processes and improve the quality of audio systems.
By applying the unit circle with tangent to real-world scenarios, students and professionals can develop a deeper understanding of its importance and utility. This powerful mathematical tool can unlock new opportunities for problem-solving and analysis, making it an invaluable asset in various fields.
Teaching Tips for Educators
Teaching the unit circle with tangent can be challenging, but with the right strategies and resources, educators can help students develop a strong understanding of this important concept. By incorporating visual aids, hands-on activities, and real-world examples, teachers can engage students and enhance their comprehension of the material.
Some teaching tips for educators include:
- Use visual aids: Incorporate diagrams, graphs, and animations to help students visualize the relationships between angles and trigonometric functions. Visual aids can make complex concepts more accessible and easier to understand.
- Encourage hands-on activities: Use interactive activities and manipulatives to help students explore the unit circle and tangent function. Hands-on experiences can reinforce learning and provide valuable practice with problem-solving skills.
- Incorporate real-world examples: Connect the unit circle with tangent to real-world scenarios and applications, demonstrating its importance and utility in various fields. Real-world examples can make the material more engaging and relevant to students.
- Provide opportunities for practice: Offer plenty of opportunities for students to practice their skills and apply their knowledge to different types of problems. Practice is essential for mastering the unit circle with tangent and developing problem-solving abilities.
By implementing these strategies, educators can create a supportive and engaging learning environment that fosters a deep understanding of the unit circle with tangent. With the right resources and approaches, students can develop the skills and confidence needed to excel in trigonometry and related fields.
Unit Circle with Tangent and Technology
Technology plays an increasingly important role in education, offering new opportunities for teaching and learning complex concepts like the unit circle with tangent. By incorporating digital tools and resources, educators can enhance their instruction and help students develop a deeper understanding of the material.
Some ways technology can be used to teach the unit circle with tangent include:
- Interactive simulations: Use online simulations and interactive tools to help students explore the unit circle and tangent function. These resources can provide a hands-on learning experience and make complex concepts more accessible.
- Educational software: Incorporate software programs that offer practice problems, quizzes, and tutorials related to the unit circle with tangent. These programs can provide valuable opportunities for practice and reinforcement of key concepts.
- Online videos and tutorials: Utilize online videos and tutorials to supplement classroom instruction and provide additional explanations of the unit circle with tangent. These resources can be particularly helpful for visual learners and students who need extra support.
- Digital assessments: Use digital assessments to track student progress and identify areas where additional support may be needed. These assessments can provide valuable feedback and help educators tailor their instruction to meet the needs of individual students.
By incorporating technology into their instruction, educators can create a more engaging and effective learning experience for students. Digital tools and resources can enhance teaching and learning, making complex concepts like the unit circle with tangent more accessible and understandable.
How Can You Practice the Unit Circle with Tangent?
Practicing the unit circle with tangent is essential for mastering this important concept and developing strong problem-solving skills. By engaging in a variety of practice activities and exercises, students can reinforce their understanding of the material and gain confidence in their abilities.
Some ways to practice the unit circle with tangent include:
- Work through practice problems: Complete practice problems related to the unit circle with tangent, focusing on different types of angles and scenarios. Practice problems can help reinforce key concepts and provide valuable opportunities for skill development.
- Create flashcards: Use flashcards to memorize key trigonometric values and relationships, such as the sine, cosine, and tangent of common angles. Flashcards can be a helpful tool for reinforcing basic knowledge and improving recall.
- Use online resources: Take advantage of online resources, such as interactive simulations and quizzes, to practice the unit circle with tangent. These resources can provide valuable opportunities for hands-on learning and skill development.
- Study with a partner: Work with a study partner to review key concepts and practice solving problems together. Collaborating with others can provide additional support and motivation for mastering the material.
By incorporating a variety of practice activities into their study routine, students can develop a strong understanding of the unit circle with tangent and improve their problem-solving skills. Consistent practice and review are essential for mastering this important mathematical concept.
Frequently Asked Questions
What is the purpose of the unit circle?
The unit circle is a fundamental concept in trigonometry, providing a simple and intuitive method for understanding the relationships between angles and trigonometric functions. It is used to calculate sine, cosine, and tangent values and visualize their behavior as angles change.
How is the tangent function different from sine and cosine?
The tangent function is defined as the ratio of sine to cosine, represented by the formula: Tangent (tan) = Sine (sin) / Cosine (cos). Unlike sine and cosine, which have maximum and minimum values, the tangent function can approach positive or negative infinity at certain angles.
What are some real-world applications of the unit circle with tangent?
The unit circle with tangent has numerous real-world applications, including navigation and GPS, architecture and construction, physics, and music and acoustics. It is an essential tool for solving complex problems and gaining insights into various fields.
How can I avoid common mistakes when working with the unit circle and tangent?
To avoid common mistakes, ensure accurate angle measurement, double-check points on the unit circle, understand the differences between sine, cosine, and tangent, and be aware of vertical asymptotes in the tangent function. Practice and attention to detail are key to mastering these concepts.
Why is it important to practice the unit circle with tangent?
Practicing the unit circle with tangent is essential for mastering the concept and developing strong problem-solving skills. Consistent practice helps reinforce understanding, improve recall of key values, and build confidence in one's abilities.
How can technology enhance learning about the unit circle with tangent?
Technology can enhance learning by providing interactive simulations, educational software, online videos and tutorials, and digital assessments. These resources can make complex concepts more accessible and engaging, helping students develop a deeper understanding of the material.
Conclusion
In conclusion, the unit circle with tangent is a powerful tool for understanding trigonometry and its applications in various fields. By mastering this concept, students and professionals can unlock new opportunities for problem-solving and analysis, enhancing their skills and knowledge in mathematics and related subjects. With the right resources, practice, and support, anyone can develop a strong understanding of the unit circle with tangent and its importance in both theoretical and practical contexts.