Calculating the area under a curve is a fundamental concept in mathematics, particularly within calculus, that finds applications in various fields such as physics, economics, and statistics. It's a powerful tool that helps in understanding the accumulation of quantities, like distance, probability, or even cost, over a given interval. Whether you're a student, a researcher, or a professional, grasping how to find the area under a curve can be incredibly beneficial.
The significance of knowing how to find the area under a curve extends beyond academic exercises. It's used to determine probabilities in statistics, compute work done by a force in physics, and even assess profit in economics. The process typically involves integration, a core part of calculus, which can seem intimidating at first. However, with a step-by-step approach, anyone can master this skill.
In this article, we'll explore various methods for calculating the area under a curve, including graphical, numerical, and analytical techniques. We'll break down each method into easy-to-understand steps and provide practical examples to solidify your understanding. By the end of this read, you'll be equipped with the knowledge and confidence to tackle problems involving the area under curves with ease.
Read also:Rock Icon Susi Quatro A Musical Force
Table of Contents
- What is the Area Under a Curve?
- Importance of Finding the Area Under a Curve
- Graphical Methods
- Numerical Methods
- Analytical Methods
- Applications in Different Fields
- How to Find Area Under a Curve?
- Common Mistakes to Avoid
- Practical Examples and Exercises
- Frequently Asked Questions
- Conclusion
What is the Area Under a Curve?
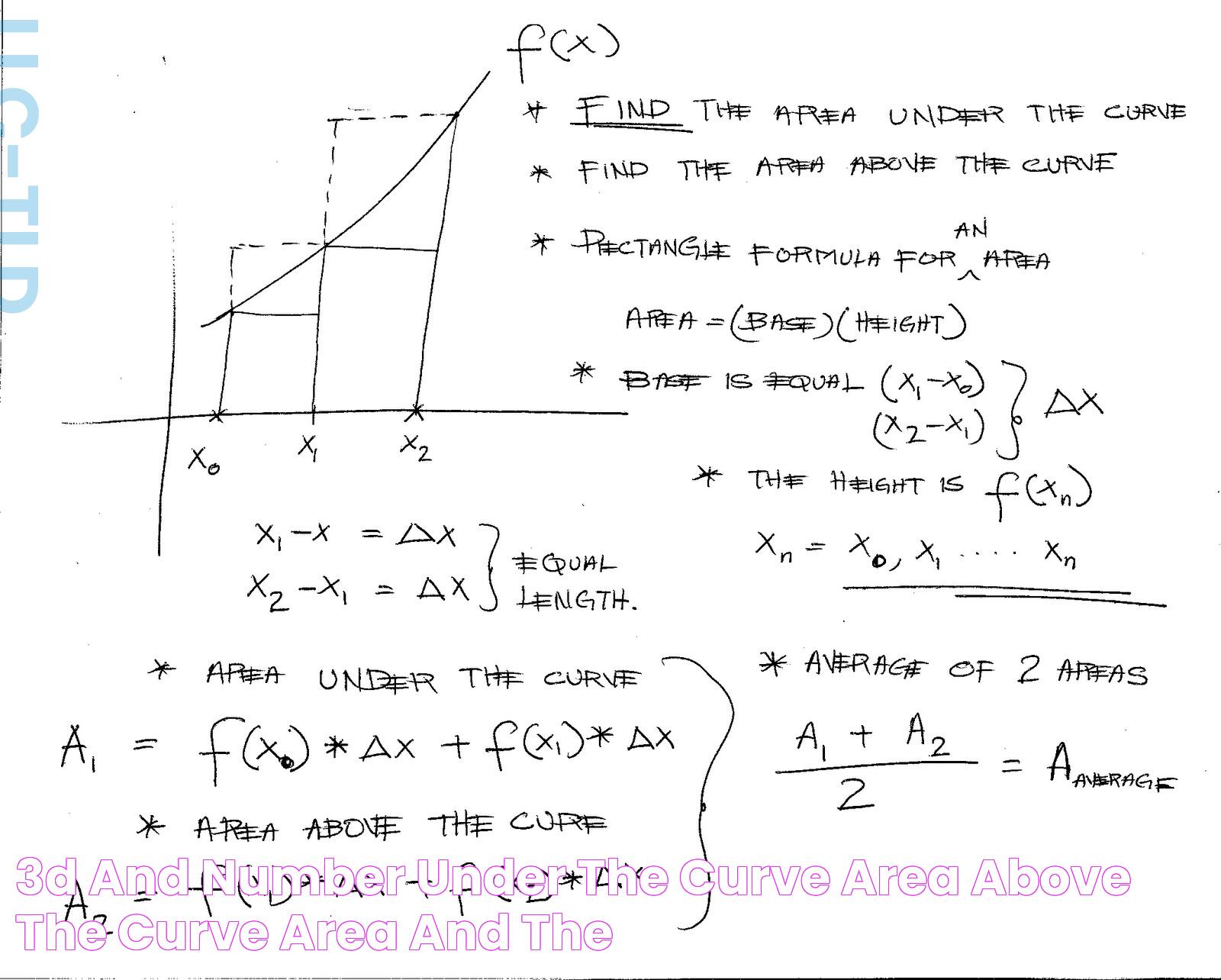
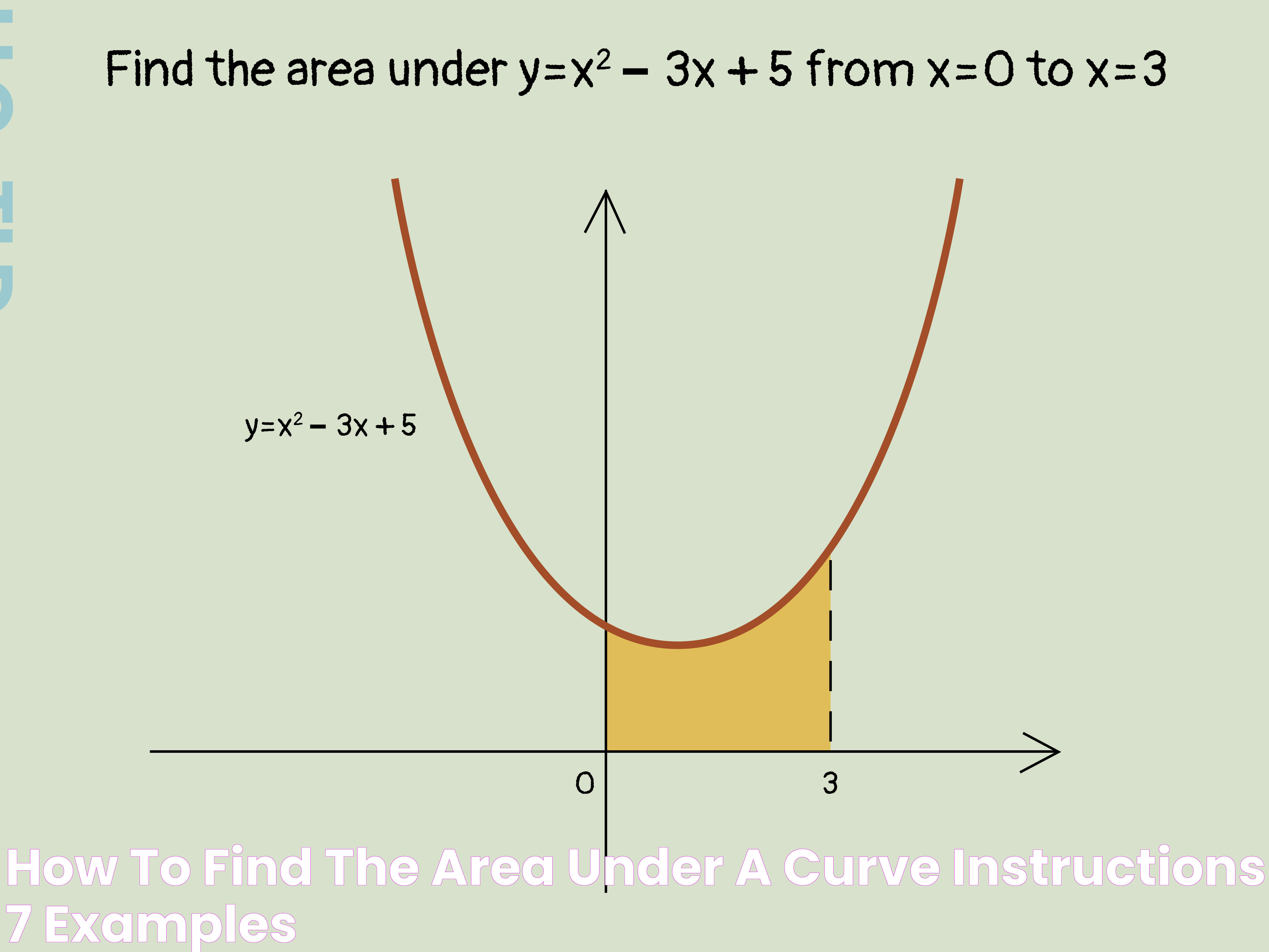
The area under a curve refers to the region enclosed by the curve itself, the x-axis, and the vertical lines at two points on the x-axis. This concept is pivotal in calculus, where it represents the integral of a function between two limits. Essentially, it's a measure of the 'total' accumulation of a quantity over a certain interval.
Calculating this area can provide insights into various physical and abstract phenomena. For instance, in physics, it can represent the distance traveled over time when interpreting a velocity-time graph. In economics, it might signify total revenue over a period given a demand curve. Understanding the area under a curve allows us to quantify these accumulations accurately.
Importance of Finding the Area Under a Curve
The ability to find the area under a curve is crucial in numerous scientific and practical applications. In physics, it's used to compute work done, heat transfer, and electrical charges. In statistics, it helps in determining probabilities and distributions. Economists use it to analyze consumer and producer surplus, among other things.
Moreover, this concept is not limited to theoretical applications. Engineers might use it to model stress-strain relationships or material properties, while ecologists could apply it to model population growth over time. The versatility of this technique underscores its importance and the need for a solid understanding of how to calculate it accurately.
Graphical Methods
Graphical methods involve using visual representations to estimate the area under a curve. These methods are particularly useful for simple functions or when a rough estimate is sufficient.
Using Geometry for Simple Areas
For curves that form simple geometric shapes, the area can be calculated using basic geometry. For instance, the area under a linear function can be calculated as a rectangle or triangle. Understanding these basic shapes and their area formulas can be handy when dealing with straightforward functions.
Read also:Is Terrifier 3 Woke Unraveling The Cultural Impact And Controversy
- Rectangles: Area = width × height
- Triangles: Area = 1/2 × base × height
- Trapezoids: Area = 1/2 × (base1 + base2) × height
Numerical Methods
When analytical solutions are hard to obtain, numerical methods offer a viable alternative. These methods approximate the area under a curve by dividing it into smaller, manageable sections.
Trapezoidal Rule
The trapezoidal rule approximates the area under a curve by dividing it into trapezoids rather than rectangles. This approach provides a more accurate approximation than simple rectangles, especially for curves that are not linear.
The area is calculated using the formula:
Area ≈ (b-a)/n * [f(a) + 2 * Σf(x_i) + f(b)]
where n is the number of subdivisions between a and b, and x_i are the points between the subdivisions.
Simpson's Rule
Simpson's Rule is another numerical method that offers higher accuracy by using parabolic arcs instead of straight lines to approximate the area. It's particularly effective for smooth, continuous functions.
The formula for Simpson's Rule is:
Area ≈ (b-a)/6 * [f(a) + 4f((a+b)/2) + f(b)]
This method provides a more precise estimate than the trapezoidal rule, especially when the function being integrated is parabolic or close to it.
Analytical Methods
Analytical methods involve the use of calculus to find the exact area under a curve. These methods require understanding the principles of integration.
Definite Integrals
A definite integral represents the exact area under a curve between two specified limits. It's evaluated using the fundamental theorem of calculus, which connects differentiation and integration.
The definite integral of a function f(x) from a to b is given by:
∫ab f(x) dx
where this integral corresponds to the net area between the curve and the x-axis over the interval [a, b].
Indefinite Integrals
An indefinite integral, on the other hand, represents a family of functions and is the antiderivative of a given function. It does not have specified limits, and its evaluation results in a general antiderivative plus a constant of integration, C.
The indefinite integral of a function f(x) is expressed as:
∫ f(x) dx = F(x) + C
where F(x) is the antiderivative of f(x).
Applications in Different Fields
The concept of finding the area under a curve extends to various real-world applications:
- Physics: Calculating work done, energy, and other physical quantities.
- Economics: Analyzing consumer and producer surplus, cost functions, and more.
- Statistics: Determining probabilities and distributions.
- Engineering: Modeling material properties and stress-strain relationships.
- Biology: Understanding population dynamics and growth models.
How to Find Area Under a Curve?
Finding the area under a curve involves choosing the right method based on the function and the context. Here's a step-by-step guide:
- Identify the function and the interval over which you need to find the area.
- Decide whether a graphical, numerical, or analytical method is appropriate.
- For simple shapes, use geometry. For more complex curves, consider numerical methods like the trapezoidal or Simpson's rule.
- If the function is integrable, use definite integrals for an exact solution.
- Calculate the integral or approximate area using the chosen method.
Common Mistakes to Avoid
When calculating the area under a curve, it's imperative to avoid common pitfalls:
- Not considering the limits of integration correctly.
- Ignoring the function's behavior outside the interval of interest.
- Overlooking the need for approximation in non-analytical methods.
- Choosing inappropriate numerical methods for the function type.
Practical Examples and Exercises
To solidify your understanding, engage in practical exercises:
- Calculate the area under the curve for f(x) = x² from x = 0 to x = 2 using different methods.
- Approximate the area under f(x) = sin(x) from x = 0 to π using the trapezoidal rule.
- Use Simpson's Rule to find the area under f(x) = e^x from x = 1 to x = 3.
Frequently Asked Questions
What is the difference between definite and indefinite integrals?
Definite integrals calculate the exact area under a curve within specific limits, while indefinite integrals provide a general antiderivative without limits.
When should I use numerical methods?
Numerical methods are ideal when analytical solutions are complex or impossible to find, providing approximations where exact solutions are difficult.
How does the trapezoidal rule differ from Simpson's rule?
The trapezoidal rule uses straight-line segments to approximate the area, while Simpson's rule uses parabolic arcs, offering higher accuracy for smoother curves.
What are some real-world applications of finding the area under a curve?
This concept is used in physics for calculating work done, in economics for surplus analysis, and in statistics for probability determinations, among others.
Can I find the area under any curve using integration?
Integration can find the area under a wide range of curves, provided they are integrable over the given interval. Some functions may require special techniques or approximations.
How do I choose the right method for finding the area under a curve?
Consider the function's complexity, the desired accuracy, and whether an exact or approximate solution is needed to choose the appropriate method.
Conclusion
Understanding how to find the area under a curve is a vital skill in mathematics with numerous practical applications. By mastering various methods, from graphical to numerical and analytical techniques, you can tackle a wide range of problems with confidence. Whether you're calculating probabilities, analyzing economic models, or solving physics problems, this knowledge will serve you well in both academic and professional settings.
**SEO Meta Description:** "Mastering the Art of Calculating the Area Under a Curve: Techniques and Insights - Discover methods to find the area under a curve with confidence and accuracy."