Square roots are fundamental mathematical concepts that play a crucial role in various fields, from science and engineering to finance and everyday problem-solving. Understanding how to find the square root can unlock a world of possibilities and simplify complex calculations. Whether you're a student, a professional, or simply curious about mathematics, learning to find square roots efficiently can enhance your analytical skills and boost your confidence in handling numerical data.
For those who may not be familiar, a square root is a number that, when multiplied by itself, results in the original number. The process of finding a square root can initially seem daunting, but with the right techniques and methods, it becomes an accessible and even enjoyable task. There are multiple ways to approach finding square roots, from manual calculations to using technological aids, each with its own set of benefits and challenges.
In this comprehensive guide, we'll explore various methods for finding square roots, offering step-by-step instructions for each approach. We'll delve into the mathematical principles that underpin square roots, discuss the historical context of their discovery, and provide practical tips for applying this knowledge in real-world scenarios. By the end of this article, you'll have a solid understanding of how to find the square root and the confidence to tackle even the most challenging problems involving square roots.
Read also:Resolving The P0171 Code Toyotas Guide To Efficient Engine Performance
Table of Contents
- What is a Square Root?
- Historical Perspective of Square Roots
- Methods of Finding Square Roots
- Manual Calculation Techniques
- Using a Calculator
- Estimation Methods
- Square Root Formulas
- How Do You Find the Square Root Efficiently?
- Application in Real Life
- Common Mistakes to Avoid
- Advanced Square Root Concepts
- Frequently Asked Questions
- Conclusion
What is a Square Root?
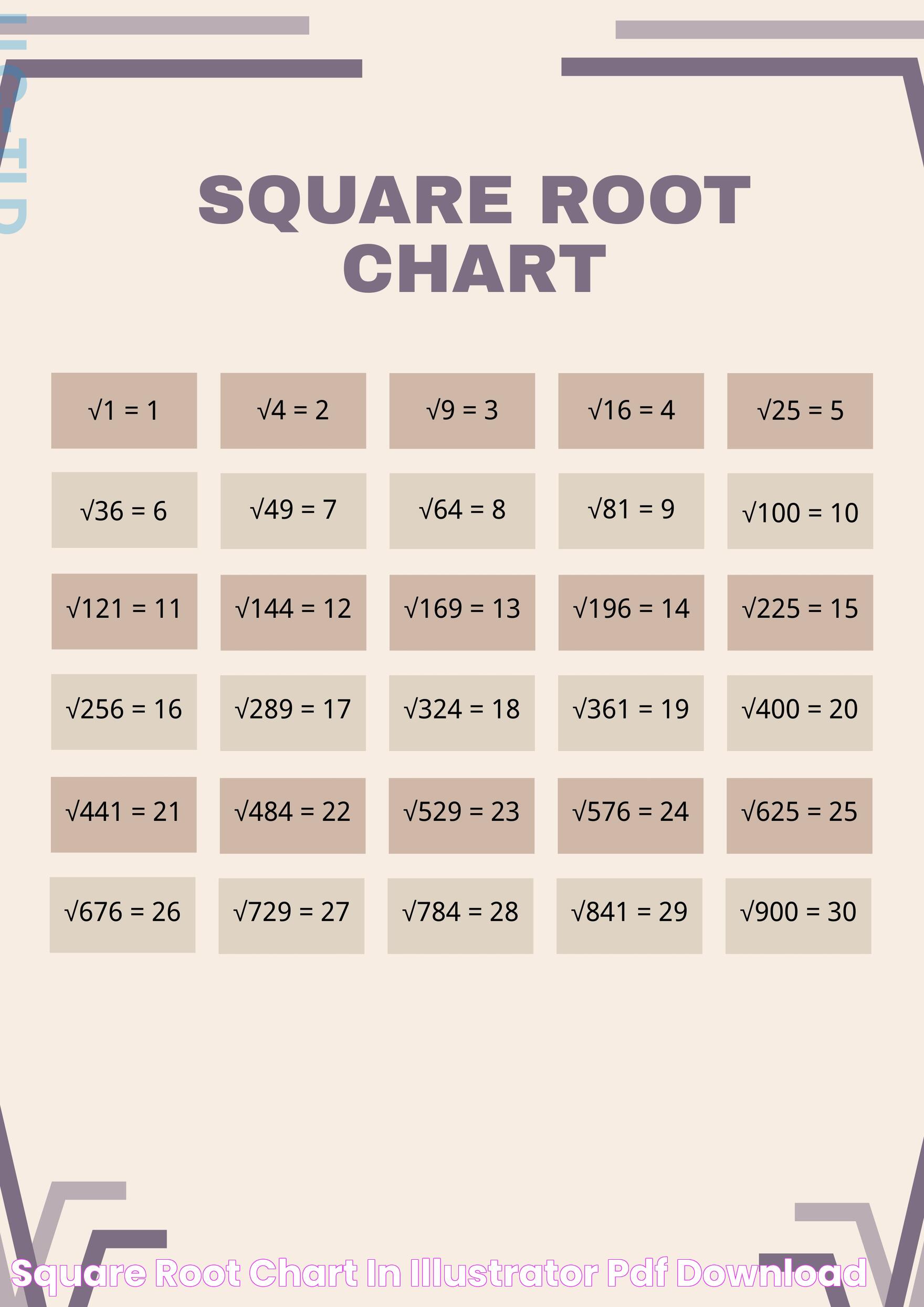
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol (√). Mathematically, if 'a' is a non-negative number, then the square root of 'a' is a number 'b' such that b² = a. For instance, the square root of 9 is 3, because 3 multiplied by 3 equals 9.
Square roots apply to both whole numbers and decimals, and they can be either positive or negative. However, in most practical applications, we focus on the principal (positive) square root. Understanding square roots is essential for solving quadratic equations, analyzing geometric shapes, and performing various scientific computations.
Historical Perspective of Square Roots
The concept of square roots has been around for thousands of years. Ancient civilizations, including the Babylonians, Egyptians, and Greeks, made significant contributions to the development of square root theory. The Babylonians, for example, had a sophisticated method for approximating square roots, recorded on clay tablets dating back to around 1800 BCE.
In ancient Greece, mathematicians like Euclid and Archimedes further explored the properties of square roots, laying the groundwork for modern algebra. The introduction of the Hindu-Arabic numeral system in Europe during the Middle Ages made calculations involving square roots more accessible, leading to significant advancements in mathematics and science.
Methods of Finding Square Roots
There are several methods for finding square roots, each with its advantages and limitations. These methods can be broadly categorized into manual techniques, calculator-assisted calculations, and estimation methods. Understanding these approaches provides a comprehensive toolkit for tackling square root problems in various contexts.
In this section, we'll delve into each method, offering step-by-step instructions and practical examples to help you master the art of finding square roots. Whether you prefer traditional mathematical techniques or modern technological aids, you'll find a method that suits your needs and skill level.
Read also:Revolutionary Non Sls Shampoo A Gentle Solution For Hair Care
Manual Calculation Techniques
Manual calculation techniques involve traditional mathematical methods for finding square roots without the aid of electronic devices. These techniques require a solid understanding of basic arithmetic operations and a keen analytical mind. While they may be time-consuming, they offer valuable insights into the underlying principles of square roots.
One popular manual technique is the long division method, which involves a series of steps to gradually approximate the square root of a number. Another approach is the prime factorization method, which breaks down the number into its prime factors and uses these to determine the square root. Both methods require practice and precision, but they are effective for finding square roots of whole numbers.
Using a Calculator
Calculators offer a quick and convenient way to find square roots, making them a popular choice for students and professionals alike. Modern calculators, including scientific and graphing models, have dedicated functions for calculating square roots, allowing users to input numbers and receive results instantly.
When using a calculator, it's essential to understand the limitations and potential sources of error. For example, calculators may round results to a certain number of decimal places, affecting the accuracy of the square root. Additionally, some calculators may not handle very large or very small numbers effectively, requiring users to apply additional techniques or tools for more complex calculations.
Estimation Methods
Estimation methods provide a way to approximate square roots when an exact value is not required or when other methods are impractical. These techniques are particularly useful in real-world scenarios where time and resources are limited, and a rough approximation is sufficient.
One common estimation method is the use of perfect squares. By identifying the closest perfect squares to the number in question, you can narrow down the range in which the square root lies. Another technique is the use of linear approximation, which involves drawing a tangent line to the curve of the square root function and using this line to estimate the square root. These methods are quick and easy to apply, making them valuable tools in diverse situations.
Square Root Formulas
Square root formulas offer mathematical shortcuts for finding square roots with greater efficiency. These formulas are based on algebraic principles and can be applied to both whole numbers and decimals, providing a versatile approach to square root calculations.
The most well-known square root formula is the Newton-Raphson method, which uses calculus to iteratively approximate the square root of a number. This formula is particularly effective for finding square roots of large numbers or numbers with many decimal places, as it converges quickly to an accurate result. Other formulas, such as the Babylonian method, offer alternative approaches with similar levels of precision and reliability.
How Do You Find the Square Root Efficiently?
Finding the square root efficiently involves selecting the right method for the task at hand and applying it with precision and accuracy. The choice of method depends on factors such as the type of number (whole or decimal), the level of precision required, and the available resources (manual calculation, calculator, or computer).
For whole numbers, manual calculation techniques like long division or prime factorization are often effective, providing insights into the structure of the number. For decimals or large numbers, calculator-assisted methods or square root formulas like the Newton-Raphson method are more suitable, as they offer faster and more accurate results.
Ultimately, the key to finding square roots efficiently is practice and familiarity with the various methods. By mastering these techniques, you'll be well-equipped to tackle square root problems in any context, whether in academic studies, professional work, or everyday life.
Application in Real Life
Square roots have numerous applications in real life, extending beyond the realm of mathematics into fields such as science, engineering, and finance. Understanding how to find square roots is essential for solving practical problems, from calculating areas and volumes to analyzing complex data sets.
In science, square roots are used in physics to calculate quantities such as velocity, acceleration, and force. In engineering, they play a crucial role in designing structures and systems, ensuring stability and efficiency. In finance, square roots are used to determine risk factors and analyze investment returns, providing insights into market trends and opportunities.
By mastering the art of finding square roots, you'll be better equipped to navigate the challenges of modern life, making informed decisions and solving problems with confidence and precision.
Common Mistakes to Avoid
When finding square roots, it's important to be aware of common mistakes that can lead to errors or inaccuracies. These mistakes often arise from misunderstandings of mathematical principles or incorrect application of techniques, and they can compromise the reliability of your results.
One common mistake is assuming that the square root of a negative number is a real number. In fact, negative numbers have no real square roots, and their square roots are classified as imaginary numbers. Another mistake is neglecting to check the precision of calculator results, which can lead to rounding errors or incorrect interpretations of data.
To avoid these pitfalls, it's essential to approach square root problems with a clear understanding of the underlying principles and a careful attention to detail. By doing so, you'll ensure that your results are accurate, reliable, and valuable in any context.
Advanced Square Root Concepts
For those seeking to deepen their understanding of square roots, there are several advanced concepts and techniques that offer new insights and challenges. These concepts go beyond the basics of square root calculation, exploring the mathematical properties and implications of square roots in greater depth.
One advanced concept is the study of irrational square roots, which cannot be expressed as exact fractions or decimals. These square roots, such as √2 or √3, have infinite non-repeating decimal expansions, and they play a crucial role in fields like number theory and geometry.
Another advanced topic is the exploration of complex square roots, which involve imaginary numbers and extend the concept of square roots into the complex plane. Understanding these concepts requires a solid foundation in algebra and calculus, but they offer valuable insights into the nature of numbers and mathematical relationships.
Frequently Asked Questions
- What is the square root of 25?
The square root of 25 is 5. This is because 5 multiplied by 5 equals 25.
- Can square roots be negative?
Square roots can be negative when considering the two possible roots of a number. For example, both 3 and -3 are square roots of 9, since (-3) × (-3) also equals 9. However, in most practical applications, we consider the principal (positive) square root.
- How do calculators find square roots?
Calculators use algorithms, such as the Newton-Raphson method, to iteratively approximate square roots. These algorithms involve complex mathematical operations that are executed quickly by the calculator's processor.
- Why are square roots important in mathematics?
Square roots are important because they are fundamental to solving quadratic equations, analyzing geometric shapes, and performing various calculations in science and engineering. They also help us understand the relationships between numbers and their properties.
- What is the difference between a square root and a cube root?
A square root is a number that, when multiplied by itself, gives the original number. A cube root is a number that, when multiplied by itself twice (i.e., raised to the third power), gives the original number. Cube roots apply to three-dimensional geometry, whereas square roots are more commonly used in two-dimensional contexts.
- Can you find the square root of a fraction?
Yes, you can find the square root of a fraction by finding the square root of the numerator and the denominator separately. For example, the square root of 1/4 is 1/2, because the square root of 1 is 1, and the square root of 4 is 2.
Conclusion
Mastering the art of finding square roots is a valuable skill that offers a multitude of benefits in both academic and professional settings. By understanding the principles behind square roots and becoming proficient in various calculation methods, you'll enhance your mathematical skills and gain confidence in tackling complex problems.
Whether you prefer manual techniques, calculator-assisted methods, or advanced mathematical formulas, the key to success lies in practice and patience. By applying these techniques regularly and exploring new concepts, you'll deepen your understanding of square roots and their applications, opening up new avenues for exploration and discovery.
In a world where mathematical literacy is increasingly important, the ability to find square roots efficiently is a powerful tool that can help you navigate the challenges of modern life with confidence and precision. Embrace the journey of learning, and unlock the potential of square roots in all their forms and applications.